Энергия электромагнитного поля. Вектор Умова. Уравнение баланса энергии (теорема Умова)

---

 

    Система основных уравнений электродинамики (1.6) —(1.9) является полной и достаточной для решения задач в самых раз­личных областях человеческой деятельности, в том числе и задач, связанных с антенно-фидерными устройствами и распростране­нием радиоволн. Однако указанная система есть система уравне­ний в частных производных, а потому допускает безграничное множество решений. Следовательно, при рассмотрении практи­ческих задач система основных уравнений должна быть дополнена рядом условий, учитывающих характер поведения поля у границ раздела сред с различными параметрами (граничные условия), поведение поля на бесконечном удалении от источника (условия излучения, принцип погашаемости, принцип предельной ампли­туды и др.) и, наконец, поведение поля в области излома образу­ющей поверхности (неаналитическое представление границы) рассматриваемого объекта, у острых кромок (условия на ребре). При решении нестационарных задач, когда зависимость полевых величин от времени явная, а не гармоническая, необходимы еще и начальные условия, т.е. значения поля в некоторый начальный момент времени (например, при t= 0). Упомянутые условия необ­ходимы для корректной постановки задачи, удовлетворяющей требованиям теоремы единственности решения уравнений Макс­велла.

О действии электромагнитного поля можно судить, как уже отмечалось, по его влиянию на движущийся заряд [см. выражение

(1.1)], а также на любое тело, находящиеся в области, занятой полем. Это действие проявляется за счет электромагнитной энер­гии W, распределенной в некоторой области V, ограниченной поверхностью S (рис. 1.5, й), причем поверхность Сможет быть как действительной (реальной), так и воображаемой (виртуаль­ной). Указанная энергия определяется выражением

Ж = (1/2)|(е_а£²+д_аЯ^гуК.                                        (1.П)

v

В пространстве она распределена с объемной плотностью

и>=(1/2)_£а£²=(1/2)ц_аЯ².                                      (1.12)

Из выражения (1.11) непосредственно следует, что энергия ЭМП И⁷представляет собою сумму энергий электрического И⁷³ и магнитного W^M полей, при этом

И⁷³ = (1/2) Je_a£W = (1/2)\EDdV;                          (1.13)

V                     V

И⁷" = (\l2)\\x_aH²dV = (1/2) J HBdV.                       (1.14)

V                         V

Энергия ЭМП И⁷ в области К может изменяться во времени за счет, по крайней мере, двух процессов. Прежде всего, она может превращаться в другие виды энергии неэлектромагнитного харак­тера, например в тепловую, химическую, биофизическую и др. Изменение количества энергии в объеме V может происходить также в результате ее ухода из объема через некоторые отверстия общей площадью 5_£ или через саму поверхности S в силу ее пол­ной или частичной прозрачности (например, за счет упомянутой воображаемости) или из-за некоторых особенностей самого поля (см. далее). Очевидно, что энергия может не только уходить из

 

 

 

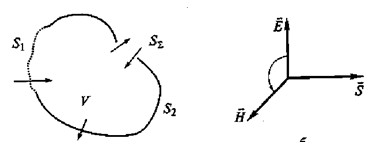
Рис 1 5 Схема произвольного объема V, замкнутого некоторой состав­ной поверхностью 5 = 5, + S₂ + S_x {а) и пояснение к определению векто­ра Умова S (б), связанного с излучением (втеканием) энергии через

отверстие S% объема V, но и входить в него извне через туже поверхность S ил и некоторую часть ее (например, через отверстия Sj).

Первый из отмеченных процессов изменения энергии ЭМП в объеме W (переход в другие виды энергии) описывается уравне­нием

P = j)EdV,                                               (1.15)

v

где Р — мощность, отдаваемая (получаемая) полем в единицу времени.

Подынтегральное выражение в уравнении (1.15) определяет объемную плотность мощности р = JE.

Энергия, уходящая (излучаемая) из объема V в единицу вре­мени (либо приходящая в него извне),

P_z=jSdS,                                                  (1.16)

s

где S — вектор Умова (рис. 1.5, б), представляющий собой плот­ность потока энергии, т.е. поток энергии, проходящей через эле­ментарную площадку dS.

Вектор Умова S определяется как векторное произведение век­торов напряженностей электрического Ё и магнитного Я полей в каждой точке поверхности S (см. рис. 1,5, б):

£ = [£,Я].                                                   (1.17)

Энергетические величины W, Р, P_z связаны между собою «ин­тегральным* соотношением — уравнением баланса энергии (теоре­мой Умова):

dW/dt + Р + Pz= 0.                                       (1.18)

По существу, это выражение закона сохранения энергии для ЭМП, который можно сформулировать так: любому изменению энергии W в некотором объеме V соответствует ее изменение за счет потерь Р или убывания (излучения) Р% во внешнее простран­ство, а также прихода энергии извне.